也许是 Intel 的广告——为什么 C++ 只比 VBA 快 4倍?(很多图)
也许是 Intel 的广告——为什么 C++ 只比 VBA 快 4倍?(很多图)

大概一年前,知乎上有个提问:为什么 C++ 只比 VBA 快 4倍? - 编程
答案里面各位专家都对问题提出了相当有效的优化方法,但却没有见到哪个回答里面有 Intel 软件的踪影。所以今天我来试着配合 Intel 的工具链来做一遍简单的优化,抛个砖,让更多人也认识到 Intel 这一系列神奇的软件。虽然,ICC 的 bug 同 MSVC/GCC 相比要更多一点,但是丝毫不妨碍它成为 Intel 架构的超级计算机的事实编译器——而且一般还会捆绑着 Intel MKL/Intel MPI 使用——benchmark 出来的 FLOPS 一眼可见得比 GCC + 其他各种 blas 高。
这段代码中,首先让我们移除 clock() 函数,改用 Intel VTune Amplifier 的计时,同时将循环扩大 100 倍让时间差异更明显,也方便 VTune 收集更多事件。
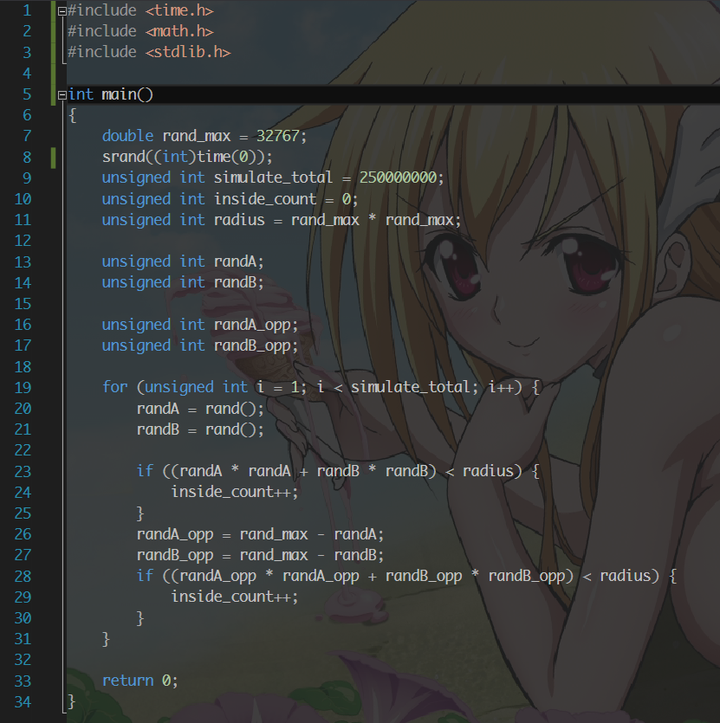
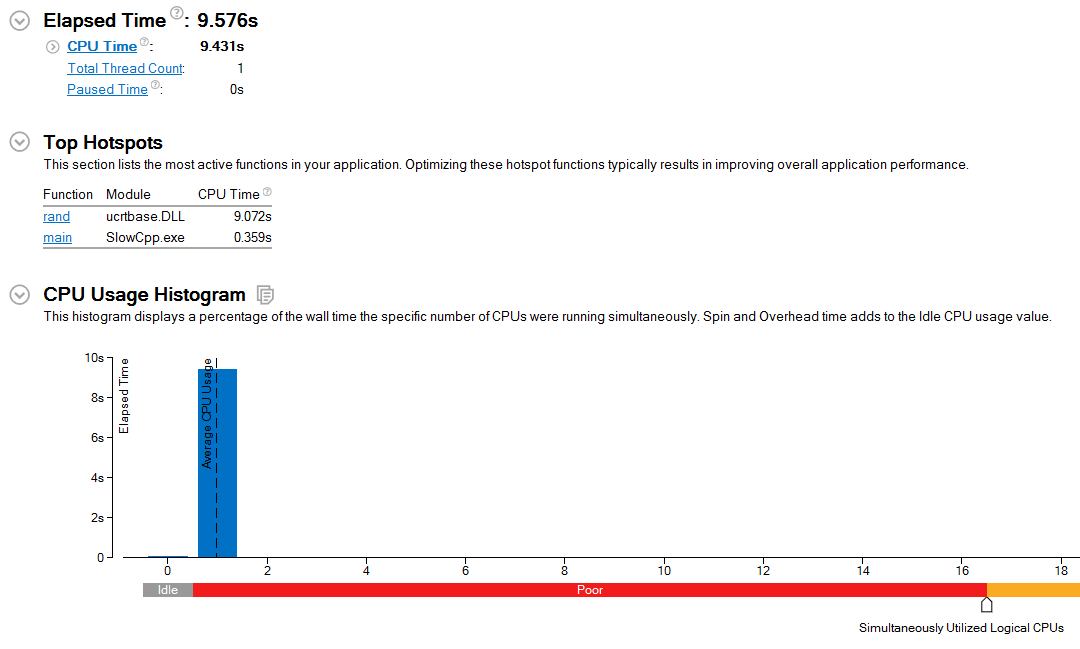
跑一遍 profiling,9.6s.
现在我们改用 Intel Compiler,时间并没有减少。(没有图)
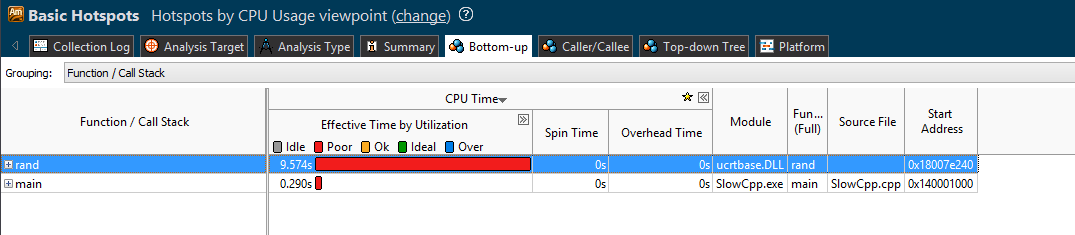
从 hotspot 图中可以看到 rand() 函数占了 9.574s. 那么我们肯定是需要更快的一个 rand.
@Milo Yip 说 “用 SSE2 + OpenMP 后及不同的随机数生成器” 是犯规,对于通用应用也许是这样,但对 HPC 应用未必尽然。编写 HPC 应用很重要的一点是要利用体系结构的特性,甚至,针对某一款 CPU 专门编写对应的代码也是可以的,不然 Intel 每次给出的新指令集岂不是都浪费了?
所以从这里开始,我们就要充分利用体系结构特性了。我现在用的电脑是 Haswell-EP 架构。
如果你对 Intel 的 Ivy Bridge 引入的指令有印象的话,或许还记得 Intel 在这一代上添加了一个硬件随机数生成器。既然有,我们当然不能浪费。让我们写一个朴素版本的 rdrand 进去:
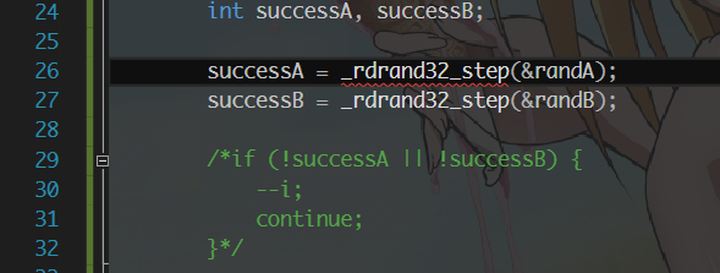
再做一遍 profiling,注意上面那段 if 在被 profile 的程序中没有被注释掉。

居然更慢了!那用它作甚?
实际上,变慢的确是预料之中,只是没有预料到变得那么慢。Hardware Random Number Generator 的意义主要在于,提供一个没有什么规律的 true random number,而加速随机数过程并不是主要目的。而且 Intel 处理器中的随机数模块并不是 on-core 的,而是每个 socket 一个,访问 latency 也高,同时,它运行在固定的 800MHz 频率上。所以,可以预见的,这个东西不会太快,再加上 if 判断的 overhead 以及我们糟糕的用法,它变得非常的慢。
当然了,这里朴素的 rdrand 的用法并不是最优的,因为我偷懒了,只写了这一个朴素的版本,实际上如果加大 pull 的宽度增加线程数量的话,我预估速度在 ~5s 左右,还是比 rand() 要快的。
一番权衡之后,我决定使用 Intel MKL 中提供的随机数生成器,顺道把类型全部改成 float. 伪随机数的生成其实是有质量的,而库提供的复杂生成器往往质量都比较高,同时运算也更加复杂,自然生成也会更慢。这里选用了 VSL_BRNG_SFMT19937 的随机数生成器,这个生成器是专门针对 SIMD 做过优化的,在快的同时而不牺牲质量。VSL 也有利用 RDRAND 的生成器,只不过比 SFMT19937 要稍慢一点。
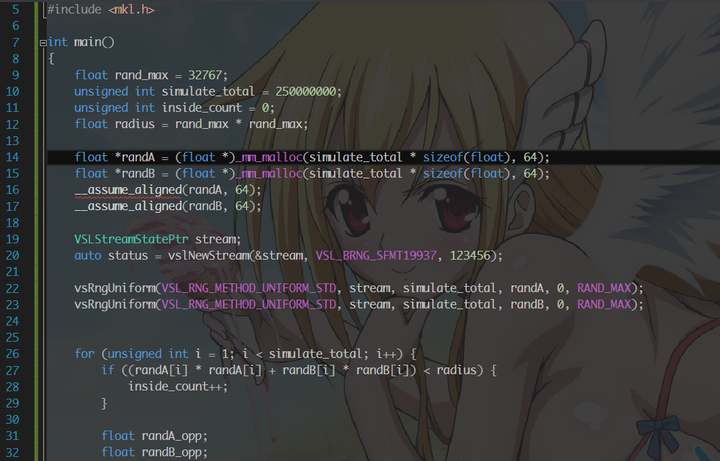
再做一遍 profiling,
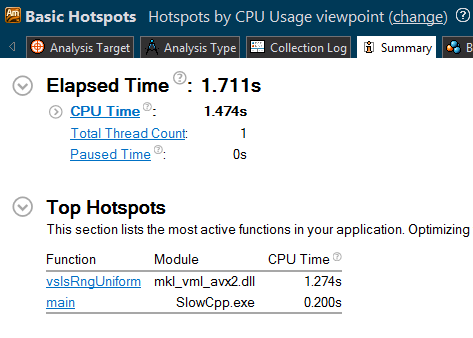
好可怕。看出来一个快速的库是多么重要了么?
接着,我们看到了大循环。有循环当然要考虑做 vectorization,充分利用 Intel 的新指令集。然而,你们真的拿衣服地以为要手动写 intrinsic 么?打开编译器的优化报告,
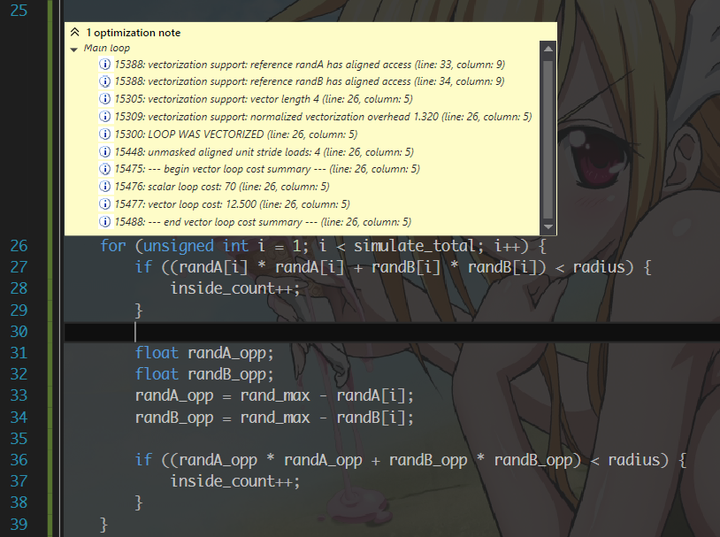
请你相信编译器的 auto-vectorization 能力。一般情况下都是不用手写向量化代码的——省力,同时也提高可读性(告诉我你们看懂 Milo 叔叔的 SSE 代码用了多久?)。当然,如果你想向女孩子展示你深厚的程序设计功底的话,手写也是可以的。还有要注意的一点是,动态分配的数组最好用 _mm_malloc 来对齐,然后写 _assume_aligned 来告诉编译器这个数组是已经对齐的了,这样向量化的效果更好。
然而这真的是我们机器的 vectorization 提升么?并不。编译器通常会选择一个比较早些的架构来进行通用的优化而不是激进地完全利用本机最新的指令集。所以我们改一个设置,让它将本机作为 target 进行优化,这样 AVX2/FMA 都可以利用上。
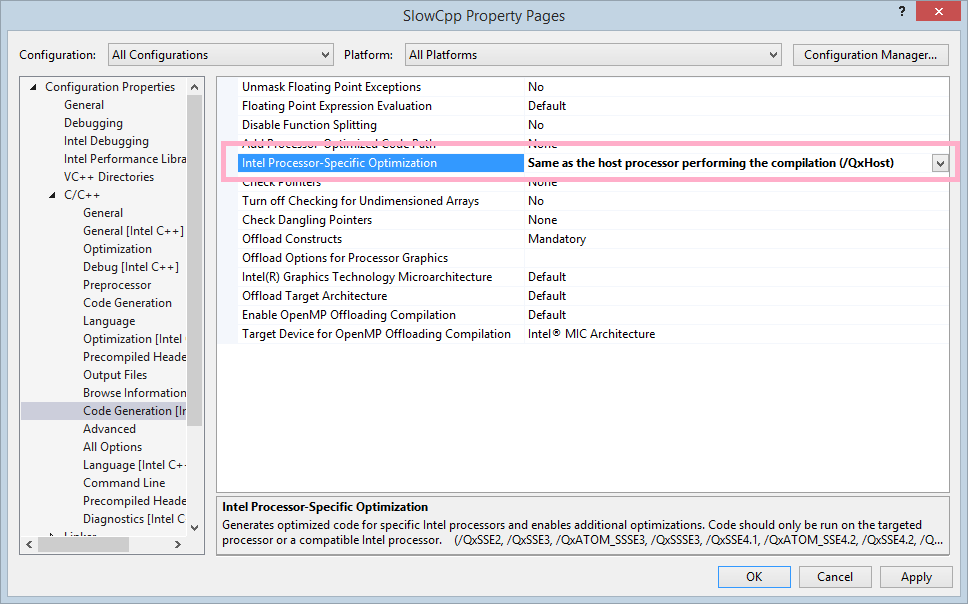
看看现在的优化报告,loop cost 是不是和上一张的不一样了?
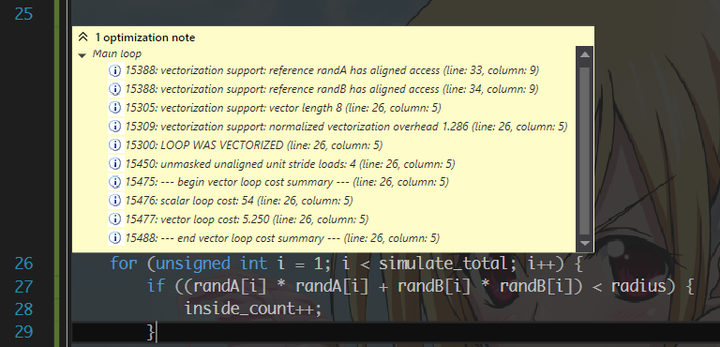
再来做一遍 profiling,性能并没有提高多少。我们发现大头其实都在那个随机数生成上面(请看上面的某张 profiling)。所以,我决定将它并行化,顺便把下面的 loop 也并行了。请注意这里我偷懒了,没有处理 simulate_total 不能被线程数量整除的情况——因为对于我的机器来说,不管 16 线程还是 32 线程都是可以被整除的所以我并不是太关心。for 的 schedule 选了 static,因为每个 loop 的计算时间基本上是相同的,所以没有必要用 dynamic 徒增 overhead (dynamic 默认的 chunksize 还是 1 哟,非常得 cache unfriendly 哟)。
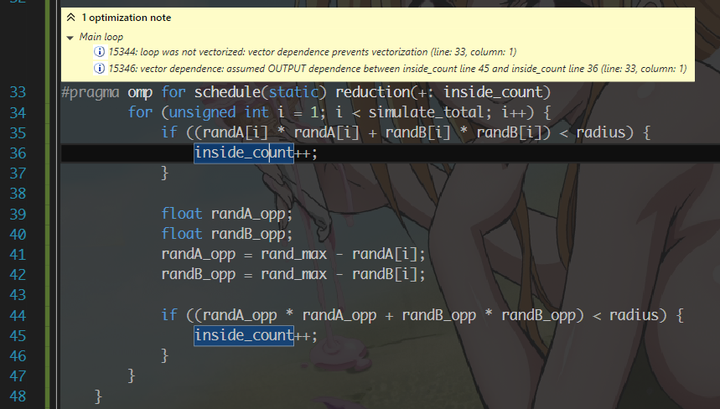
编译,哎呀,编译器说有 dependence. 怎么办呢?我们这会先不管这个 vectorization,先来 profile 一遍并行过的版本。
咦,跟上面的 1.7s 比好像更慢了?让我们先来调整一下线程数量吧。我的电脑是16核32线程的,OpenMP 默认会开满 32 线程,所以我手动把它改成 16 的。在程序开头添加两行代码:
_putenv("KMP_AFFINITY=granularity=fine,scatter");
omp_set_num_threads(16);第一行意思是将线程均匀分布在处理器上(所以每个核心都能分到一个线程而不是堆在一起),第二行是设置 16 线程。
看,更快了吧,但是 0.4s 的提升也反映出这里并行的意义并不太大。为什么线程数少了反而更快了呢?因为每核心的 SIMD unit 其实只有一个,所以如果开了超线程,两个线程都跑满,核心的计算单元就被 oversubscribe 了,再加上 spinlock 吃满资源还不让出时间片,只会拖累运行速度。这也就是为什么很多超级计算机都把超线程功能从 BIOS 里面关掉了,这个东西,日常用着好用,但做计算的时候反而是个拖累。
好了,让我们回到 vectorization 问题去。以往遇到 dependence 问题的时候,我们都会人工分析确认是不是有这些 dependence,如果没有的话则标记 #pragma ivdep 指示编译器这里没有 dependence. 但是现在有个问题是,这里我们用了 OpenMP reduction,这个东西在出现 dependence 时,有时候坑会很大。所以为了方便起见,我移除了 reduction,同时把 inside_count 拆成了上下两份。这还没完,我们一共有 16 个线程,那我把两个 inside_count 分别做成 16 元素的数组,让各个线程一个萝卜一个坑地往里面填,最后在外面另用一个 loop 求和,并不会增加多少 overhead.
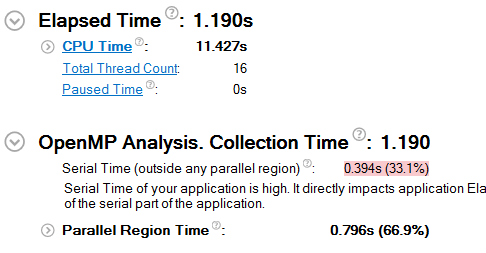
现在运行时间已经缩短到 1.19 秒了。还能不能更快?
其实到这里已经很快了,MKL 的随机数生成器是一个比较安全的高质量生成器。但是如果想要更快的话,我们可以选择不是那么随机的,比如@Milo Yip 提供的,简单随机数生成器。不过好孩子们可不要学习哟,尤其是,Milo 叔叔向量化的代码有好几个 seed 哟,是好几个 rng 同时在生成哟,而 seed 选取不当的话,伪随机数的分布可就不再是 uniform 了哒哟,结果就不会再那么正确了哟。事实上,Milo 叔叔提供的代码,运行出来的结果是 3.14082. 这还只是 128 位的 SSE 指令集,而如果加宽 vector 的话,random distribution 误差还会更大,从而加大结果的误差。不过目前这个精度来看,一般应用的要求还是可以满足的。
我试了下 Milo 叔叔的 RNG,向量化以后大概能达到 0.25s 的速度,相比较于 1.19s 来说提升还是挺大的。顺道改了一下 seed,准确度有些提升。而且,这是我们扩大 100 倍 simulate_total 的计时,要注意我们的运行时间只能和其它的 VTune 计时一起参考——因为 VTune 计数的是整个程序的运行时间——包括程序启动退出等,同时, VTune 对程序的运行速度也有影响。
从这里也能看出来,MKL 的随机数生成器其实是高度优化过的了,速度非常快,并不输简单 RNG 太多。而下面的计算,瓶颈主要是那些圆内圆外的判断上,VTune 给出的报告中,pipeline stall 的原因里,bad speculation 占了很大一部分,而这显然也是我们无法改善的——毕竟都是随机数。
正如 @grapeot 叔叔说的,遇到性能问题,第一反应应当是用 profiler 看看瓶颈到底在哪,而且一个经验是这个瓶颈往往是很难猜的——比如这个例子,我们各种优化算半径的那部分,带来的提升远不如将 rand() 换成 MKL 提供的 PRNG.
我们上面用的是 Windows 平台的 VS 和 Intel 工具链,方便好用但也非常贵。如果是 Linux 平台下可以用 Intel 的 Linux 工具链,Mac 下可以用 Intel 的 Mac 工具链,但基本思路都是一样的。
最后,让我引用一下 @空明流转 的话来结束这篇文章。现代体系结构已经高度复杂,时间空间上各种优化手段都会相互依赖相互制约,即便 case 比较简单,想直接推理硬件行为也是一件很困难的事情。这个时候,简单的 profiling 比一切臆想都要有用的多,虽然它常常也是不准的。最好的优化,还是 boosting:写十个方案,选一个最好的。文章中没有向大家展示出其它几个版本的源代码——因为我懒得截图了,你们知道曾经有过,而且没有现在这个快,就可以了。
而最简单的优化——你也可以看出来源码并没有什么大改动,就是用信得过的处理器厂商(不是 A 开头的)提供的自家的工具链和性能库——毕竟爹最清楚儿子平时做事都是个什么熊样。
感谢您的阅读,这里是 low performance computing specialist 坂本番茄酱,我们下次再见。
附录
这里献上手写的 AVX2/FMA 代码。因为用时已经很短了,线程调度只会增加 overhead,所以就不再并行化了。
https://gist.github.com/sakamoto-poteko/9d45efde2a1f728a6f6c
照顾墙,贴在下面:
#include <stdlib.h>
#include <stdio.h>
#include <immintrin.h>
const static __m256i SEED_MUL = _mm256_set1_epi32(214013);
const static __m256i SEED_ADDI = _mm256_set1_epi32(2531011);
const static __m256i SEED_MASK = _mm256_set1_epi32(0x3F800000);
const static __m256 FLOAT_1 = _mm256_set1_ps(1.f);
const static __m256i INT32_1 = _mm256_set1_epi32(1);
inline __m256 rand_avx2(__m256i &seed)
{
__m256i vr0 = _mm256_mullo_epi32(seed, SEED_MUL);
__m256i vr1 = _mm256_add_epi32(vr0, SEED_ADDI);
__m256i vr2 = _mm256_srli_epi32(vr1, 9);
__m256i vr3 = _mm256_or_si256(vr2, SEED_MASK);
__m256 vr4 = _mm256_castsi256_ps(vr3);
__m256 result = _mm256_sub_ps(vr4, FLOAT_1);
seed = vr1;
return result;
}
double simulate(__m256i seedA, __m256i seedB)
{
const unsigned simulate_total = 250000000;
__m256i inside_count = _mm256_set1_epi32(0);
__m256i inside_count_opp = _mm256_set1_epi32(0);
for (unsigned i = 1; i < simulate_total / 8; i++) {
__m256 vecA = rand_avx2(seedA);
__m256 vecB = rand_avx2(seedB);
__m256 squareA = _mm256_mul_ps(vecA, vecA);
__m256 len = _mm256_fmadd_ps(vecB, vecB, squareA); // vecB * vecB + squareA
__m256 compMask = _mm256_cmp_ps(len, FLOAT_1, _CMP_LT_OS);
__m256i result = _mm256_and_si256(_mm256_castps_si256(compMask), INT32_1);
inside_count = _mm256_add_epi32(inside_count, result);
__m256 vecA_opp = _mm256_sub_ps(FLOAT_1, vecA);
__m256 vecB_opp = _mm256_sub_ps(FLOAT_1, vecB);
__m256 squareA_opp = _mm256_mul_ps(vecA_opp, vecA_opp);
__m256 len_opp = _mm256_fmadd_ps(vecB_opp, vecB_opp, squareA_opp); // vecB * vecB + squareA
__m256 compMask_opp = _mm256_cmp_ps(len_opp, FLOAT_1, _CMP_LT_OS);
__m256i result_opp = _mm256_and_si256(_mm256_castps_si256(compMask_opp), INT32_1);
inside_count_opp = _mm256_add_epi32(inside_count_opp, result_opp);
}
unsigned __int64 total = 0;
for (int i = 0; i < 8; ++i) {
total += inside_count.m256i_u32[i] + inside_count_opp.m256i_u32[i];
}
return total / double(simulate_total) * 2;
}
int main()
{
__m256i a;
_rdrand64_step(a.m256i_u64);
_rdrand64_step(a.m256i_u64 + 1);
_rdrand64_step(a.m256i_u64 + 2);
_rdrand64_step(a.m256i_u64 + 3);
__m256i b;
_rdrand64_step(b.m256i_u64);
_rdrand64_step(b.m256i_u64 + 1);
_rdrand64_step(b.m256i_u64 + 2);
_rdrand64_step(b.m256i_u64 + 3);
double result = simulate(a, b);
fprintf(stderr, "%f\n", result);
return 0;
}